null and alternative hypothesis calculator online

Hypothesis Testing Calculator

Type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

One Sample T Test Calculator

Enter sample data, reporting results in apa style, one sample t-test, what is a one sample t-test, how to use the one sample t test calculator, calculators.

“extremely user friendly”

“truly amazing!”

“so easy to use!”

Statistics Calculator

You want to analyze your data effortlessly? DATAtab makes it easy and online.

Online Statistics Calculator

What do you want to calculate online? The online statistics calculator is simple and uncomplicated! Here you can find a list of all implemented methods!

Create charts online with DATAtab

Create your charts for your data directly online and uncomplicated. To do this, insert your data into the table under Charts and select which chart you want.

The advantages of DATAtab

Statistics, as simple as never before..

DATAtab is a modern statistics software, with unique user-friendliness. Statistical analyses are done with just a few clicks, so DATAtab is perfect for statistics beginners and for professionals who want more flow in the user experience.

Directly in the browser, fully flexible.

Directly in the browser, fully flexible. DATAtab works directly in your web browser. You have no installation and maintenance effort whatsoever. Wherever and whenever you want to use DATAtab, just go to the website and get started.

All the statistical methods you need.

DATAtab offers you a wide range of statistical methods. We have selected the most central and best known statistical methods for you and do not overwhelm you with special cases.

Data security is a top priority.

All data that you insert and evaluate on DATAtab always remain on your end device. The data is not sent to any server or stored by us (not even temporarily). Furthermore, we do not pass on your data to third parties in order to analyze your user behavior.

Many tutorials with simple examples.

In order to facilitate the introduction, DATAtab offers a large number of free tutorials with focused explanations in simple language. We explain the statistical background of the methods and give step-by-step explanations for performing the analyses in the statistics calculator.

Practical Auto-Assistant.

DATAtab takes you by the hand in the world of statistics. When making statistical decisions, such as the choice of scale or measurement level or the selection of suitable methods, Auto-Assistants ensure that you get correct results quickly.

Charts, simple and clear.

With DATAtab data visualization is fun! Here you can easily create meaningful charts that optimally illustrate your results.

New in the world of statistics?

DATAtab was primarily designed for people for whom statistics is new territory. Beginners are not overwhelmed with a lot of complicated options and checkboxes, but are encouraged to perform their analyses step by step.

Online survey very simple.

DATAtab offers you the possibility to easily create an online survey, which you can then evaluate immediately with DATAtab.

Our references

Alternative to statistical software like SPSS and STATA

DATAtab was designed for ease of use and is a compelling alternative to statistical programs such as SPSS and STATA. On datatab.net, data can be statistically evaluated directly online and very easily (e.g. t-test, regression, correlation etc.). DATAtab's goal is to make the world of statistical data analysis as simple as possible, no installation and easy to use. Of course, we would also be pleased if you take a look at our second project Statisty .

Extensive tutorials

Descriptive statistics.

Here you can find out everything about location parameters and dispersion parameters and how you can describe and clearly present your data using characteristic values.

Hypothesis Test

Here you will find everything about hypothesis testing: One sample t-test , Unpaired t-test , Paired t-test and Chi-square test . You will also find tutorials for non-parametric statistical procedures such as the Mann-Whitney u-Test and Wilcoxon-Test . mann-whitney-u-test and the Wilcoxon test

The regression provides information about the influence of one or more independent variables on the dependent variable. Here are simple explanations of linear regression and logistic regression .

Correlation

Correlation analyses allow you to analyze the linear association between variables. Learn when to use Pearson correlation or Spearman rank correlation . With partial correlation , you can calculate the correlation between two variables to the exclusion of a third variable.

Partial Correlation

The partial correlation shows you the correlation between two variables to the exclusion of a third variable.

Levene Test

The Levene Test checks your data for variance equality. Thus, the levene test is used as a prerequisite test for many hypothesis tests .

The p-value is needed for every hypothesis test to be able to make a statement whether the null hypothesis is accepted or rejected.

Distributions

DATAtab provides you with tables with distributions and helpful explanations of the distribution functions. These include the Table of t-distribution and the Table of chi-squared distribution

Contingency table

With a contingency table you can get an overview of two categorical variables in the statistics.

Equivalence and non-inferiority

In an equivalence trial, the statistical test aims at showing that two treatments are not too different in characteristics and a non-inferiority trial wants to show that an experimental treatment is not worse than an established treatment.

If there is a clear cause-effect relationship between two variables, then we can speak of causality. Learn more about causality in our tutorial.

Multicollinearity

Multicollinearity is when two or more independent variables have a high correlation.

Effect size for independent t-test

Learn how to calculate the effect size for the t-test for independent samples.

Reliability analysis calculator

On DATAtab, Cohen's Kappa can be easily calculated online in the Cohen’s Kappa Calculator . there is also the Fleiss Kappa Calculator . Of course, the Cronbach's alpha can also be calculated in the Cronbach's Alpha Calculator .

Analysis of variance with repeated measurement

Repeated measures ANOVA tests whether there are statistically significant differences in three or more dependent samples.

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net

One sample t test calculator

The One Sample t Test Calculator allows you to determine p-values, critical values, test statistics, and conclusions using the one-sample t test method.

Related Calculators :

• List of all calculator
• P-value calculator
• Critical value Calculator
• One sample z test calculator

How to Use the One Sample t Test Calculator

• Select Data Type: Choose whether to input summary statistics directly or provide a data set.
• Input Your Data: Enter the required values such as population mean, sample size, sample mean, and sample standard deviation.
• Set Hypotheses: Specify the null and alternative hypotheses.
• Calculate: Click the "Calculate" button to see the test statistic, p-value, and other relevant results.

Interpreting the Results

To interpret the results of a one-sample t-test, you must first grasp several crucial components: the test statistic (t-value), degrees of freedom, p-value, and confidence interval. Here's a step-by-step way to interpreting these findings:

Components of One-Sample t-Test Results

Test Statistic (t-value) :

This result indicates the amount of standard deviations your sample mean is from the population mean under the null hypothesis. A larger absolute value of t indicates a wider divergence between the sample mean and the population average.

Degrees of Freedom (df):

This is normally the sample size less one (n-1). The degrees of freedom are utilized to calculate the critical value of t using the t-distribution table.

This represents the likelihood of receiving a test statistic as extreme as the one observed, assuming the null hypothesis is correct. A low p-value ( less than 0.05) indicates that the observed data are unlikely to support the null hypothesis, resulting in its rejection.

Confidence Interval:

This defines a range of values within which the genuine population mean is expected to fall. If the confidence interval excludes the population mean stated in the null hypothesis, it supports the conclusion that the sample mean differs considerably from the population mean.

Steps to Interpret the Results

State the Hypotheses:

Null Hypothesis (H₀): The population mean is equal to a specified value (e.g. \( \mu=\mu_0 \) ).

Alternative Hypothesis (H₁): The population mean is different from the specified value (e.g. \( \mu \ne \mu_0 \) ).

Check the t-value:

Compare the t-value to the crucial value from the t-distribution table based on the specified significance level (α, typically 0.05) and degrees of freedom.

If |t-value| > critical value, reject the null hypothesis.

Examine the P-value:

• If the p-value is less than the chosen significance level \( \alpha \), reject the null hypothesis.
• A p-value less than \(0.05\) typically indicates strong evidence against the null hypothesis.

Review the Confidence Interval:

Check to see if the confidence interval for the sample mean includes the population mean under the null hypothesis.

If the interval excludes the population mean, it indicates that the sample mean is significantly different than the population mean.

Requirements and Assumptions for a one sample t test

To effectively execute and interpret a one-sample t-test, you must first grasp the test's requirements and assumptions. Meeting these parameters assures that the test results are legitimate and reliable.

Requirements for a One-Sample t-Test

You will need a sample of the population you are studying.

To compare the sample mean to the population mean (μ₀), you must have a known population mean.

A suitable sample size is necessary. While the t-test performs well with small sample sizes, higher sample sizes yield more accurate results.

Assumptions of a One-Sample t-Test

Random Sampling:

Data should be acquired from the population using random sampling. This guarantees that the sample is representative of the population and minimises bias.

Scale of Measurement:

The data must be continuous (interval or ratio scale). This means that the data points may be meaningfully arranged, and the differences between them are consistent and observable.

The data should follow a roughly normal distribution. This assumption is particularly essential for small sample sizes (n < 30). For bigger samples, the Central Limit Theorem predicts that the sample mean distribution will be essentially normal, regardless of the distribution of the data.

Independence :

Observations in the sample must be independent of one another. This means that the value of one observation should not affect or predict the value of another.

Unknown Population Standard Deviation: :

The test assumes that the population standard deviation \(\alpha\) is unknown and needs to be determined from the sample.

Applications of the One Sample t Test

This test is widely used in various fields including:

• Education: Assessing whether the average test scores of a class differ from the national average.
• Healthcare: Comparing the mean blood pressure level of a group of patients to a known population mean.
• Business: Evaluating if the average sales of a product differ from the company's historical sales data.

Frequently Asked Questions (FAQs)

What is a one-sample t test.

A one-sample t test is a statistical approach for determining whether a sample's mean differs significantly from a known population mean.

When should I use a one-sample t test?

Use this test when the population standard deviation is unknown and the sample size is small (typically n < 30).

How do I interpret the p-value in a t test?

The p-value indicates the probability of observing the test results under the null hypothesis. A low p-value less than the significance level equal to \( \alpha \) suggests rejecting the null hypothesis.

Why Use Our One Sample t Test Calculator?

Our calculator offers several advantages:

• Accuracy: Provides precise calculations for your hypothesis testing needs.
• User-Friendly Interface: Easy to navigate and input your data.
• Educational Value: Offers detailed explanations and step-by-step guides to help you understand the results.
• Time-Saving: Quickly computes results, allowing you to focus on analysis and interpretation.
• Versatility: Suitable for various fields such as education, healthcare, and business, making it a valuable tool for a wide range of users.

Start your hypothesis testing today with our One Sample t Test Calculator and achieve accurate and reliable results effortlessly.

Hypothesis Testing

Hypothesis testing calculator, hypothesis testing is a fundamental statistical method used to make inferences or conclusions about a population based on sample data. it provides a structured framework for determining whether there is enough evidence to support or refute a specific claim or hypothesis. whether conducting scientific research, analyzing business data, or evaluating experimental results, hypothesis testing helps you make informed decisions by assessing the validity of assumptions., how to use hypothesis testing tool.

Hypothesis Testing involves a series of steps to evaluate a hypothesis and determine whether to accept or reject it based on sample data. Here’s a simplified guide to conducting hypothesis testing:

• Formulate Hypotheses: Begin by stating the null hypothesis (H0) and alternative hypotheses (H1). The null hypothesis represents the default assumption or no effect, while the alternative hypothesis represents the effect or difference you are testing for.
• Choose the Significance Level: Select a significance level (α), commonly set at 0.05 or 5%. This represents the probability of rejecting the null hypothesis when it is true (Type I error).
• Collect and Analyze Data: Gather sample data relevant to your hypothesis. Perform the appropriate statistical test (e.g., t-test, chi-square test) to analyze the data and calculate the test statistic.
• Calculate the P-value: Determine the p-value, which indicates the probability of observing the test results or more extreme results if the null hypothesis is true.
• Make a Decision: Compare the p-value to the significance level. If the p-value is less than the significance level, reject the null hypothesis. Otherwise, accept it.

Based on your decision, conclude the hypothesis and discuss the implications of your findings.

For example, a manufacturer claims that their light bulbs have a lifespan of 1,000 hours. You want to test if the actual lifespan differs from this claim.

The tool will send you some data when you input your 1000 hours of lifespan. Below, we have discussed the result scenarios and told you the best steps to take. 

• Null Hypothesis (H0): The average lifespan of the light bulbs is 1,000 hours.
• Alternative Hypothesis (H1): The average lifespan of the light bulbs is not 1,000 hours.

Significance Level

• Significance Level (α): 0.05

Analyze Data

• Sample Data: Lifespan of 10 light bulbs (in hours): 995, 1,010, 1,020, 1,015, 1,005, 990, 1,030, 1,025, 1,040, 1,000
• Perform a t-test to compare the sample mean to the claimed mean (1,000 hours).

Make a Decision

• If the p-value from the t-test is less than 0.05, reject the null hypothesis.
• If the null hypothesis is rejected, it means there is significant evidence to suggest the average lifespan differs from 1,000 hours.

How Hypothesis Testing is Helpful?

Supports evidence-based decisions.

Hypothesis Testing provides a structured approach to making data-based decisions. It helps validate claims and assumptions with statistical evidence, leading to more informed choices.

Ensures Rigorous Analysis

By using hypothesis testing, you apply rigorous statistical methods to analyze data. This reduces the risk of making decisions based on unreliable or misleading results.

Facilitates Research and Development

In research and development, hypothesis testing helps evaluate new theories, products, or interventions. It provides a scientific basis for determining their effectiveness or impact.

Improves Business Strategies

Businesses use hypothesis testing to assess the effectiveness of marketing campaigns, product changes, or operational improvements. It helps in optimizing strategies based on data-driven insights.

Enhances Accuracy and Reliability

Hypothesis testing helps maintain accuracy and reliability in research findings and data analysis. It ensures that conclusions drawn are statistically valid and not due to random chance.

Wrapping Up!

In conclusion, Hypothesis Testing is a crucial statistical method for evaluating hypotheses and making data-driven decisions. It provides a systematic approach to testing assumptions and assessing evidence, supporting accurate conclusions in various fields such as research, business, and development. By applying hypothesis testing, you can enhance the validity and reliability of your findings and make well-informed decisions based on statistical analysis.

Related Statistical Calculators

Privacy overview.

p-value Calculator

Table of contents

Welcome to our p-value calculator! You will never again have to wonder how to find the p-value, as here you can determine the one-sided and two-sided p-values from test statistics, following all the most popular distributions: normal, t-Student, chi-squared, and Snedecor's F.

P-values appear all over science, yet many people find the concept a bit intimidating. Don't worry – in this article, we will explain not only what the p-value is but also how to interpret p-values correctly . Have you ever been curious about how to calculate the p-value by hand? We provide you with all the necessary formulae as well!

🙋 If you want to revise some basics from statistics, our normal distribution calculator is an excellent place to start.

What is p-value?

Formally, the p-value is the probability that the test statistic will produce values at least as extreme as the value it produced for your sample . It is crucial to remember that this probability is calculated under the assumption that the null hypothesis H 0 is true !

More intuitively, p-value answers the question:

Assuming that I live in a world where the null hypothesis holds, how probable is it that, for another sample, the test I'm performing will generate a value at least as extreme as the one I observed for the sample I already have?

It is the alternative hypothesis that determines what "extreme" actually means , so the p-value depends on the alternative hypothesis that you state: left-tailed, right-tailed, or two-tailed. In the formulas below, S stands for a test statistic, x for the value it produced for a given sample, and Pr(event | H 0 ) is the probability of an event, calculated under the assumption that H 0 is true:

Left-tailed test: p-value = Pr(S ≤ x | H 0 )

Right-tailed test: p-value = Pr(S ≥ x | H 0 )

Two-tailed test:

p-value = 2 × min{Pr(S ≤ x | H 0 ), Pr(S ≥ x | H 0 )}

(By min{a,b} , we denote the smaller number out of a and b .)

If the distribution of the test statistic under H 0 is symmetric about 0 , then: p-value = 2 × Pr(S ≥ |x| | H 0 )

or, equivalently: p-value = 2 × Pr(S ≤ -|x| | H 0 )

As a picture is worth a thousand words, let us illustrate these definitions. Here, we use the fact that the probability can be neatly depicted as the area under the density curve for a given distribution. We give two sets of pictures: one for a symmetric distribution and the other for a skewed (non-symmetric) distribution.

• Symmetric case: normal distribution:

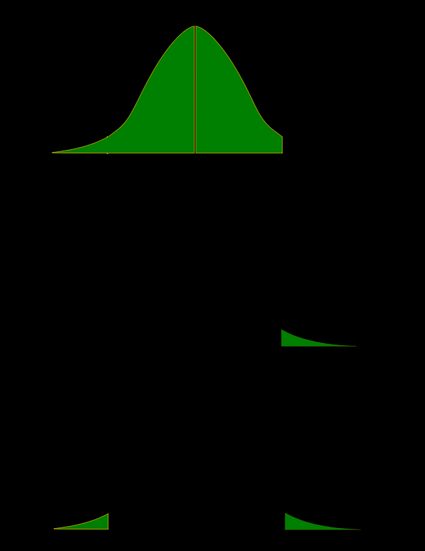
• Non-symmetric case: chi-squared distribution:

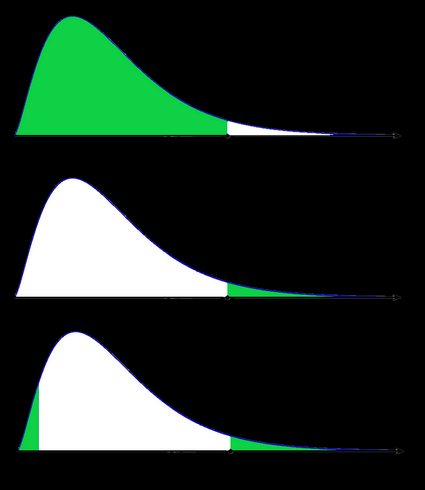
In the last picture (two-tailed p-value for skewed distribution), the area of the left-hand side is equal to the area of the right-hand side.

How do I calculate p-value from test statistic?

To determine the p-value, you need to know the distribution of your test statistic under the assumption that the null hypothesis is true . Then, with the help of the cumulative distribution function ( cdf ) of this distribution, we can express the probability of the test statistics being at least as extreme as its value x for the sample:

Left-tailed test:

p-value = cdf(x) .

Right-tailed test:

p-value = 1 - cdf(x) .

p-value = 2 × min{cdf(x) , 1 - cdf(x)} .

If the distribution of the test statistic under H 0 is symmetric about 0 , then a two-sided p-value can be simplified to p-value = 2 × cdf(-|x|) , or, equivalently, as p-value = 2 - 2 × cdf(|x|) .

The probability distributions that are most widespread in hypothesis testing tend to have complicated cdf formulae, and finding the p-value by hand may not be possible. You'll likely need to resort to a computer or to a statistical table, where people have gathered approximate cdf values.

Well, you now know how to calculate the p-value, but… why do you need to calculate this number in the first place? In hypothesis testing, the p-value approach is an alternative to the critical value approach . Recall that the latter requires researchers to pre-set the significance level, α, which is the probability of rejecting the null hypothesis when it is true (so of type I error ). Once you have your p-value, you just need to compare it with any given α to quickly decide whether or not to reject the null hypothesis at that significance level, α. For details, check the next section, where we explain how to interpret p-values.

How to interpret p-value

As we have mentioned above, the p-value is the answer to the following question:

What does that mean for you? Well, you've got two options:

• A high p-value means that your data is highly compatible with the null hypothesis; and
• A small p-value provides evidence against the null hypothesis , as it means that your result would be very improbable if the null hypothesis were true.

However, it may happen that the null hypothesis is true, but your sample is highly unusual! For example, imagine we studied the effect of a new drug and got a p-value of 0.03 . This means that in 3% of similar studies, random chance alone would still be able to produce the value of the test statistic that we obtained, or a value even more extreme, even if the drug had no effect at all!

The question "what is p-value" can also be answered as follows: p-value is the smallest level of significance at which the null hypothesis would be rejected. So, if you now want to make a decision on the null hypothesis at some significance level α , just compare your p-value with α :

• If p-value ≤ α , then you reject the null hypothesis and accept the alternative hypothesis; and
• If p-value ≥ α , then you don't have enough evidence to reject the null hypothesis.

Obviously, the fate of the null hypothesis depends on α . For instance, if the p-value was 0.03 , we would reject the null hypothesis at a significance level of 0.05 , but not at a level of 0.01 . That's why the significance level should be stated in advance and not adapted conveniently after the p-value has been established! A significance level of 0.05 is the most common value, but there's nothing magical about it. Here, you can see what too strong a faith in the 0.05 threshold can lead to. It's always best to report the p-value, and allow the reader to make their own conclusions.

Also, bear in mind that subject area expertise (and common reason) is crucial. Otherwise, mindlessly applying statistical principles, you can easily arrive at statistically significant, despite the conclusion being 100% untrue.

How to use the p-value calculator to find p-value from test statistic

As our p-value calculator is here at your service, you no longer need to wonder how to find p-value from all those complicated test statistics! Here are the steps you need to follow:

Pick the alternative hypothesis : two-tailed, right-tailed, or left-tailed.

Tell us the distribution of your test statistic under the null hypothesis: is it N(0,1), t-Student, chi-squared, or Snedecor's F? If you are unsure, check the sections below, as they are devoted to these distributions.

If needed, specify the degrees of freedom of the test statistic's distribution.

Enter the value of test statistic computed for your data sample.

By default, the calculator uses the significance level of 0.05.

Our calculator determines the p-value from the test statistic and provides the decision to be made about the null hypothesis.

How do I find p-value from z-score?

In terms of the cumulative distribution function (cdf) of the standard normal distribution, which is traditionally denoted by Φ , the p-value is given by the following formulae:

Left-tailed z-test:

p-value = Φ(Z score )

Right-tailed z-test:

p-value = 1 - Φ(Z score )

Two-tailed z-test:

p-value = 2 × Φ(−|Z score |)

p-value = 2 - 2 × Φ(|Z score |)

🙋 To learn more about Z-tests, head to Omni's Z-test calculator .

We use the Z-score if the test statistic approximately follows the standard normal distribution N(0,1) . Thanks to the central limit theorem, you can count on the approximation if you have a large sample (say at least 50 data points) and treat your distribution as normal.

A Z-test most often refers to testing the population mean , or the difference between two population means, in particular between two proportions. You can also find Z-tests in maximum likelihood estimations.

How do I find p-value from t?

The p-value from the t-score is given by the following formulae, in which cdf t,d stands for the cumulative distribution function of the t-Student distribution with d degrees of freedom:

Left-tailed t-test:

p-value = cdf t,d (t score )

Right-tailed t-test:

p-value = 1 - cdf t,d (t score )

Two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

p-value = 2 - 2 × cdf t,d (|t score |)

Use the t-score option if your test statistic follows the t-Student distribution . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails – the exact shape depends on the parameter called the degrees of freedom . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from the normal distribution N(0,1).

The most common t-tests are those for population means with an unknown population standard deviation, or for the difference between means of two populations , with either equal or unequal yet unknown population standard deviations. There's also a t-test for paired (dependent) samples .

🙋 To get more insights into t-statistics, we recommend using our t-test calculator .

p-value from chi-square score (χ² score)

Use the χ²-score option when performing a test in which the test statistic follows the χ²-distribution .

This distribution arises if, for example, you take the sum of squared variables, each following the normal distribution N(0,1). Remember to check the number of degrees of freedom of the χ²-distribution of your test statistic!

How to find the p-value from chi-square-score ? You can do it with the help of the following formulae, in which cdf χ²,d denotes the cumulative distribution function of the χ²-distribution with d degrees of freedom:

Left-tailed χ²-test:

p-value = cdf χ²,d (χ² score )

Right-tailed χ²-test:

p-value = 1 - cdf χ²,d (χ² score )

Remember that χ²-tests for goodness-of-fit and independence are right-tailed tests! (see below)

Two-tailed χ²-test:

p-value = 2 × min{cdf χ²,d (χ² score ), 1 - cdf χ²,d (χ² score )}

(By min{a,b} , we denote the smaller of the numbers a and b .)

The most popular tests which lead to a χ²-score are the following:

Testing whether the variance of normally distributed data has some pre-determined value. In this case, the test statistic has the χ²-distribution with n - 1 degrees of freedom, where n is the sample size. This can be a one-tailed or two-tailed test .

Goodness-of-fit test checks whether the empirical (sample) distribution agrees with some expected probability distribution. In this case, the test statistic follows the χ²-distribution with k - 1 degrees of freedom, where k is the number of classes into which the sample is divided. This is a right-tailed test .

Independence test is used to determine if there is a statistically significant relationship between two variables. In this case, its test statistic is based on the contingency table and follows the χ²-distribution with (r - 1)(c - 1) degrees of freedom, where r is the number of rows, and c is the number of columns in this contingency table. This also is a right-tailed test .

p-value from F-score

Finally, the F-score option should be used when you perform a test in which the test statistic follows the F-distribution , also known as the Fisher–Snedecor distribution. The exact shape of an F-distribution depends on two degrees of freedom .

To see where those degrees of freedom come from, consider the independent random variables X and Y , which both follow the χ²-distributions with d 1 and d 2 degrees of freedom, respectively. In that case, the ratio (X/d 1 )/(Y/d 2 ) follows the F-distribution, with (d 1 , d 2 ) -degrees of freedom. For this reason, the two parameters d 1 and d 2 are also called the numerator and denominator degrees of freedom .

The p-value from F-score is given by the following formulae, where we let cdf F,d1,d2 denote the cumulative distribution function of the F-distribution, with (d 1 , d 2 ) -degrees of freedom:

Left-tailed F-test:

p-value = cdf F,d1,d2 (F score )

Right-tailed F-test:

p-value = 1 - cdf F,d1,d2 (F score )

Two-tailed F-test:

p-value = 2 × min{cdf F,d1,d2 (F score ), 1 - cdf F,d1,d2 (F score )}

Below we list the most important tests that produce F-scores. All of them are right-tailed tests .

A test for the equality of variances in two normally distributed populations . Its test statistic follows the F-distribution with (n - 1, m - 1) -degrees of freedom, where n and m are the respective sample sizes.

ANOVA is used to test the equality of means in three or more groups that come from normally distributed populations with equal variances. We arrive at the F-distribution with (k - 1, n - k) -degrees of freedom, where k is the number of groups, and n is the total sample size (in all groups together).

A test for overall significance of regression analysis . The test statistic has an F-distribution with (k - 1, n - k) -degrees of freedom, where n is the sample size, and k is the number of variables (including the intercept).

With the presence of the linear relationship having been established in your data sample with the above test, you can calculate the coefficient of determination, R 2 , which indicates the strength of this relationship . You can do it by hand or use our coefficient of determination calculator .

A test to compare two nested regression models . The test statistic follows the F-distribution with (k 2 - k 1 , n - k 2 ) -degrees of freedom, where k 1 and k 2 are the numbers of variables in the smaller and bigger models, respectively, and n is the sample size.

You may notice that the F-test of an overall significance is a particular form of the F-test for comparing two nested models: it tests whether our model does significantly better than the model with no predictors (i.e., the intercept-only model).

Can p-value be negative?

No, the p-value cannot be negative. This is because probabilities cannot be negative, and the p-value is the probability of the test statistic satisfying certain conditions.

What does a high p-value mean?

A high p-value means that under the null hypothesis, there's a high probability that for another sample, the test statistic will generate a value at least as extreme as the one observed in the sample you already have. A high p-value doesn't allow you to reject the null hypothesis.

What does a low p-value mean?

A low p-value means that under the null hypothesis, there's little probability that for another sample, the test statistic will generate a value at least as extreme as the one observed for the sample you already have. A low p-value is evidence in favor of the alternative hypothesis – it allows you to reject the null hypothesis.

What do you want?

What do you know?

Your Z-score

Z-score : the test statistic follows the standard normal distribution N(0,1).

.css-m482sy.css-m482sy{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-m482sy.css-m482sy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-m482sy .js-external-link-button.link-like,.css-m482sy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-m482sy .js-external-link-button.link-like:hover,.css-m482sy .js-external-link-anchor:hover,.css-m482sy .js-external-link-button.link-like:active,.css-m482sy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-m482sy .js-external-link-button.link-like:focus-visible,.css-m482sy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-m482sy p,.css-m482sy div{margin:0;display:block;}.css-m482sy pre{margin:0;display:block;}.css-m482sy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-m482sy pre:not(:first-child){padding-top:8px;}.css-m482sy ul,.css-m482sy ol{display:block margin:0;padding-left:20px;}.css-m482sy ul li,.css-m482sy ol li{padding-top:8px;}.css-m482sy ul ul,.css-m482sy ol ul,.css-m482sy ul ol,.css-m482sy ol ol{padding-top:0;}.css-m482sy ul:not(:first-child),.css-m482sy ol:not(:first-child){padding-top:4px;} .css-1h42f0z{margin:auto;overflow:auto;overflow-wrap:break-word;word-break:break-word;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-1h42f0z .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-1h42f0z .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-1h42f0z .katex .katex-version::after{content:'0.13.13';}.css-1h42f0z .katex .katex-mathml{position:absolute;clip:rect(1px,1px,1px,1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-1h42f0z .katex .katex-html>.newline{display:block;}.css-1h42f0z .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-1h42f0z .katex .strut{display:inline-block;}.css-1h42f0z .katex .textbf{font-weight:bold;}.css-1h42f0z .katex .textit{font-style:italic;}.css-1h42f0z .katex .textrm{font-family:KaTeX_Main;}.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .texttt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-1h42f0z .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-1h42f0z .katex .mathrm{font-style:normal;}.css-1h42f0z .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-1h42f0z .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-1h42f0z .katex .amsrm{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathbb,.css-1h42f0z .katex .textbb{font-family:KaTeX_AMS;}.css-1h42f0z .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-1h42f0z .katex .mathfrak,.css-1h42f0z .katex .textfrak{font-family:KaTeX_Fraktur;}.css-1h42f0z .katex .mathtt{font-family:KaTeX_Typewriter;}.css-1h42f0z .katex .mathscr,.css-1h42f0z .katex .textscr{font-family:KaTeX_Script;}.css-1h42f0z .katex .mathsf,.css-1h42f0z .katex .textsf{font-family:KaTeX_SansSerif;}.css-1h42f0z .katex .mathboldsf,.css-1h42f0z .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-1h42f0z .katex .mathitsf,.css-1h42f0z .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-1h42f0z .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-1h42f0z .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-1h42f0z .katex .vlist-r{display:table-row;}.css-1h42f0z .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-1h42f0z .katex .vlist>span{display:block;height:0;position:relative;}.css-1h42f0z .katex .vlist>span>span{display:inline-block;}.css-1h42f0z .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-1h42f0z .katex .vlist-t2{margin-right:-2px;}.css-1h42f0z .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-1h42f0z .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-1h42f0z .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-1h42f0z .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-1h42f0z .katex .msupsub{text-align:left;}.css-1h42f0z .katex .mfrac>span>span{text-align:center;}.css-1h42f0z .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .mfrac .frac-line,.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline,.css-1h42f0z .katex .hdashline,.css-1h42f0z .katex .rule{min-height:1px;}.css-1h42f0z .katex .mspace{display:inline-block;}.css-1h42f0z .katex .llap,.css-1h42f0z .katex .rlap,.css-1h42f0z .katex .clap{width:0;position:relative;}.css-1h42f0z .katex .llap>.inner,.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{position:absolute;}.css-1h42f0z .katex .llap>.fix,.css-1h42f0z .katex .rlap>.fix,.css-1h42f0z .katex .clap>.fix{display:inline-block;}.css-1h42f0z .katex .llap>.inner{right:0;}.css-1h42f0z .katex .rlap>.inner,.css-1h42f0z .katex .clap>.inner{left:0;}.css-1h42f0z .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-1h42f0z .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-1h42f0z .katex .overline .overline-line,.css-1h42f0z .katex .underline .underline-line,.css-1h42f0z .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-1h42f0z .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-1h42f0z .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-1h42f0z .katex .sizing.reset-size1.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size1.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size1.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-1h42f0z .katex .sizing.reset-size1.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size1.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size1.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size1.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size1.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size1.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-1h42f0z .katex .sizing.reset-size1.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-1h42f0z .katex .sizing.reset-size1.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-1h42f0z .katex .sizing.reset-size2.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size2.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size2.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-1h42f0z .katex .sizing.reset-size2.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size2.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size2.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-1h42f0z .katex .sizing.reset-size2.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-1h42f0z .katex .sizing.reset-size2.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-1h42f0z .katex .sizing.reset-size2.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-1h42f0z .katex .sizing.reset-size2.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-1h42f0z .katex .sizing.reset-size2.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-1h42f0z .katex .sizing.reset-size3.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-1h42f0z .katex .sizing.reset-size3.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size3.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-1h42f0z .katex .sizing.reset-size3.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-1h42f0z .katex .sizing.reset-size3.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-1h42f0z .katex .sizing.reset-size3.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-1h42f0z .katex .sizing.reset-size3.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-1h42f0z .katex .sizing.reset-size3.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-1h42f0z .katex .sizing.reset-size3.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-1h42f0z .katex .sizing.reset-size3.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-1h42f0z .katex .sizing.reset-size4.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size4.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size4.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-1h42f0z .katex .sizing.reset-size4.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size4.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-1h42f0z .katex .sizing.reset-size4.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-1h42f0z .katex .sizing.reset-size4.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-1h42f0z .katex .sizing.reset-size4.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-1h42f0z .katex .sizing.reset-size4.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-1h42f0z .katex .sizing.reset-size4.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-1h42f0z .katex .sizing.reset-size4.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-1h42f0z .katex .sizing.reset-size5.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size5.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size5.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-1h42f0z .katex .sizing.reset-size5.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-1h42f0z .katex .sizing.reset-size5.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size5.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-1h42f0z .katex .sizing.reset-size5.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-1h42f0z .katex .sizing.reset-size5.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-1h42f0z .katex .sizing.reset-size5.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-1h42f0z .katex .sizing.reset-size5.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-1h42f0z .katex .sizing.reset-size5.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-1h42f0z .katex .sizing.reset-size6.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size6.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-1h42f0z .katex .sizing.reset-size6.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-1h42f0z .katex .sizing.reset-size6.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-1h42f0z .katex .sizing.reset-size6.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-1h42f0z .katex .sizing.reset-size6.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size6.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size6.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size6.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-1h42f0z .katex .sizing.reset-size6.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-1h42f0z .katex .sizing.reset-size6.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-1h42f0z .katex .sizing.reset-size7.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size7.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-1h42f0z .katex .sizing.reset-size7.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-1h42f0z .katex .sizing.reset-size7.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-1h42f0z .katex .sizing.reset-size7.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-1h42f0z .katex .sizing.reset-size7.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size7.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size7.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size7.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-1h42f0z .katex .sizing.reset-size7.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-1h42f0z .katex .sizing.reset-size7.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-1h42f0z .katex .sizing.reset-size8.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size8.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-1h42f0z .katex .sizing.reset-size8.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-1h42f0z .katex .sizing.reset-size8.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-1h42f0z .katex .sizing.reset-size8.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-1h42f0z .katex .sizing.reset-size8.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size8.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size8.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size8.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-1h42f0z .katex .sizing.reset-size8.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-1h42f0z .katex .sizing.reset-size8.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-1h42f0z .katex .sizing.reset-size9.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-1h42f0z .katex .sizing.reset-size9.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-1h42f0z .katex .sizing.reset-size9.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-1h42f0z .katex .sizing.reset-size9.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-1h42f0z .katex .sizing.reset-size9.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-1h42f0z .katex .sizing.reset-size9.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-1h42f0z .katex .sizing.reset-size9.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-1h42f0z .katex .sizing.reset-size9.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-1h42f0z .katex .sizing.reset-size9.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size9.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-1h42f0z .katex .sizing.reset-size9.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-1h42f0z .katex .sizing.reset-size10.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-1h42f0z .katex .sizing.reset-size10.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-1h42f0z .katex .sizing.reset-size10.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-1h42f0z .katex .sizing.reset-size10.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-1h42f0z .katex .sizing.reset-size10.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-1h42f0z .katex .sizing.reset-size10.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-1h42f0z .katex .sizing.reset-size10.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-1h42f0z .katex .sizing.reset-size10.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-1h42f0z .katex .sizing.reset-size10.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-1h42f0z .katex .sizing.reset-size10.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-1h42f0z .katex .sizing.reset-size10.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-1h42f0z .katex .sizing.reset-size11.size1,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-1h42f0z .katex .sizing.reset-size11.size2,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-1h42f0z .katex .sizing.reset-size11.size3,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-1h42f0z .katex .sizing.reset-size11.size4,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-1h42f0z .katex .sizing.reset-size11.size5,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-1h42f0z .katex .sizing.reset-size11.size6,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-1h42f0z .katex .sizing.reset-size11.size7,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-1h42f0z .katex .sizing.reset-size11.size8,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-1h42f0z .katex .sizing.reset-size11.size9,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-1h42f0z .katex .sizing.reset-size11.size10,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-1h42f0z .katex .sizing.reset-size11.size11,.css-1h42f0z .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-1h42f0z .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-1h42f0z .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-1h42f0z .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-1h42f0z .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-1h42f0z .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-1h42f0z .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-1h42f0z .katex .delimcenter{position:relative;}.css-1h42f0z .katex .op-symbol{position:relative;}.css-1h42f0z .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-1h42f0z .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-1h42f0z .katex .op-limits>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent>.vlist-t{text-align:center;}.css-1h42f0z .katex .accent .accent-body{position:relative;}.css-1h42f0z .katex .accent .accent-body:not(.accent-full){width:0;}.css-1h42f0z .katex .overlay{display:block;}.css-1h42f0z .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-1h42f0z .katex .mtable .arraycolsep{display:inline-block;}.css-1h42f0z .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-1h42f0z .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-1h42f0z .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-1h42f0z .katex .svg-align{text-align:left;}.css-1h42f0z .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-1h42f0z .katex svg path{stroke:none;}.css-1h42f0z .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-1h42f0z .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-1h42f0z .katex .stretchy::before,.css-1h42f0z .katex .stretchy::after{content:'';}.css-1h42f0z .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-1h42f0z .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-1h42f0z .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-1h42f0z .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-1h42f0z .katex .x-arrow-pad{padding:0 0.5em;}.css-1h42f0z .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-1h42f0z .katex .x-arrow,.css-1h42f0z .katex .mover,.css-1h42f0z .katex .munder{text-align:center;}.css-1h42f0z .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-1h42f0z .katex .fbox,.css-1h42f0z .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-1h42f0z .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-1h42f0z .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-1h42f0z .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-1h42f0z .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-1h42f0z .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-1h42f0z .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-1h42f0z .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-1h42f0z .katex .mtr-glue{width:50%;}.css-1h42f0z .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-1h42f0z .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-1h42f0z .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-1h42f0z .katex-display{display:block;margin:1em 0;text-align:center;}.css-1h42f0z .katex-display>.katex{display:block;white-space:nowrap;}.css-1h42f0z .katex-display>.katex>.katex-html{display:block;position:relative;}.css-1h42f0z .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-1h42f0z .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-1h42f0z .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-1h42f0z body{counter-reset:katexEqnNo mmlEqnNo;}.css-1h42f0z .link-like{color:#007bff;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-1h42f0z code,.css-1h42f0z kbd,.css-1h42f0z pre,.css-1h42f0z samp{font-family:monospace;}.css-1h42f0z code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-1h42f0z figcaption,.css-1h42f0z caption{text-align:center;}.css-1h42f0z figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-1h42f0z h3{font-size:1.75rem;}.css-1h42f0z h4{font-size:1.5rem;}.css-1h42f0z .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-1h42f0z .mathBlock .katex{font-size:24px;text-align:left;}.css-1h42f0z .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-1h42f0z .videoBlock,.css-1h42f0z .imageBlock{margin-bottom:16px;}.css-1h42f0z .imageBlock__image-align--left,.css-1h42f0z .videoBlock__video-align--left{float:left;}.css-1h42f0z .imageBlock__image-align--right,.css-1h42f0z .videoBlock__video-align--right{float:right;}.css-1h42f0z .imageBlock__image-align--center,.css-1h42f0z .videoBlock__video-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-1h42f0z .imageBlock__image-align--none,.css-1h42f0z .videoBlock__video-align--none{clear:both;margin-left:0;margin-right:0;}.css-1h42f0z .videoBlock__video--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-1h42f0z .videoBlock__video--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-1h42f0z .videoBlock__caption{text-align:left;}.css-1h42f0z table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-1h42f0z .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-1h42f0z .tableBlock thead,.css-1h42f0z .tableBlock thead th{border-bottom:1px solid #333!important;}.css-1h42f0z .tableBlock th,.css-1h42f0z .tableBlock td{padding:10px;text-align:left;}.css-1h42f0z .tableBlock th{font-weight:bold!important;}.css-1h42f0z .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-1h42f0z .tableBlock caption>p{margin:0;}.css-1h42f0z .tableBlock th>p,.css-1h42f0z .tableBlock td>p{margin:0;}.css-1h42f0z .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-1h42f0z .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-1h42f0z .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-1h42f0z .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-1h42f0z .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-1h42f0z .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-1h42f0z .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-1h42f0z .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-1h42f0z .tableBlock [data-text-align='center']{text-align:center;}.css-1h42f0z .tableBlock [data-text-align='left']{text-align:left;}.css-1h42f0z .tableBlock [data-text-align='right']{text-align:right;}.css-1h42f0z .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-1h42f0z .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-1h42f0z .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-1h42f0z .tableBlock__font-size--xxsmall{font-size:10px;}.css-1h42f0z .tableBlock__font-size--xsmall{font-size:12px;}.css-1h42f0z .tableBlock__font-size--small{font-size:14px;}.css-1h42f0z .tableBlock__font-size--large{font-size:18px;}.css-1h42f0z .tableBlock__border--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-1h42f0z .tableBlock__border--bordered td,.css-1h42f0z .tableBlock__border--bordered th{border:1px solid #e2e5e7;}.css-1h42f0z .tableBlock__border--borderless tbody+tbody,.css-1h42f0z .tableBlock__border--borderless td,.css-1h42f0z .tableBlock__border--borderless th,.css-1h42f0z .tableBlock__border--borderless tr,.css-1h42f0z .tableBlock__border--borderless thead,.css-1h42f0z .tableBlock__border--borderless thead th{border:0!important;}.css-1h42f0z .tableBlock:not(.tableBlock__table-striped) tbody tr{background-color:unset!important;}.css-1h42f0z .tableBlock__table-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-1h42f0z .tableBlock__table-compactl th,.css-1h42f0z .tableBlock__table-compact td{padding:3px!important;}.css-1h42f0z .tableBlock__full-size{width:100%;}.css-1h42f0z .textBlock{margin-bottom:16px;}.css-1h42f0z .textBlock__text-formatting--finePrint{font-size:12px;}.css-1h42f0z .textBlock__text-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-1h42f0z .textBlock__text-infoBox p{margin:0;}.css-1h42f0z .textBlock__text-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-1h42f0z .textBlock__text-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-1h42f0z .textBlock__text-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-1h42f0z .textBlock__text-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-1h42f0z .textBlock__text-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-1h42f0z .textBlock__text-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-1h42f0z .textBlock__text-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-1h42f0z.css-1h42f0z{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-1h42f0z.css-1h42f0z:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-1h42f0z .js-external-link-button.link-like,.css-1h42f0z .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-1h42f0z .js-external-link-button.link-like:hover,.css-1h42f0z .js-external-link-anchor:hover,.css-1h42f0z .js-external-link-button.link-like:active,.css-1h42f0z .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-1h42f0z .js-external-link-button.link-like:focus-visible,.css-1h42f0z .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-1h42f0z p,.css-1h42f0z div{margin:0;display:block;}.css-1h42f0z pre{margin:0;display:block;}.css-1h42f0z pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-1h42f0z pre:not(:first-child){padding-top:8px;}.css-1h42f0z ul,.css-1h42f0z ol{display:block margin:0;padding-left:20px;}.css-1h42f0z ul li,.css-1h42f0z ol li{padding-top:8px;}.css-1h42f0z ul ul,.css-1h42f0z ol ul,.css-1h42f0z ul ol,.css-1h42f0z ol ol{padding-top:0;}.css-1h42f0z ul:not(:first-child),.css-1h42f0z ol:not(:first-child){padding-top:4px;} Interpretation

Significance level α